แจกฟรี แนวข้อสอบ เจ้าพนักงานสถิติ กระทรวงสาธารณสุข สสจ

สถิติ(Statistic)

สถิติ (Statistics) หมายถึง

               1.) ตัวเลขแทนปริมาณจำนวนข้อมูล หรือข้อเท็จจริงของสิ่งต่าง ๆ ที่คนโดยทั่วไปต้องการศึกษาหาความรู้ เช่นต้องการทราบปริมาณน้ำฝนที่ตกในกรุงเทพมหานครปี 2541 เป็นต้น

               2)  ค่าตัวเลขที่เกิดจากการคำนวณมาจากกลุ่มตัวอย่าง (Sample) หรือคิดมาจากนิยามทางคณิตศาสตร์ เช่นคำนวณหาค่าเฉลี่ย ค่าความแปรปรวน ค่าที่คำนวณได้เรียกว่าค่าสถิติ (A Statistic) ส่วนค่าสถิติทั้งหลายเรียกว่า ค่าสถิติหลาย ๆ ค่า (Statistics)

               3) วิชาการแขนงหนึ่งที่จัดเป็นวิชาวิทยาศาสตร์ และเป็นทั้งวิทยาศาสตร์บริสุทธิ์และวิทยาศาสตร์ประยุกต์ และยังหมายรวมถึงระเบียบวิธีการสถิติอันประกอบไปด้วยขั้นตอน 4 ขั้นตอนที่ใช้ในการศึกษาได้แก่

                             1. การเก็บรวบรวมข้อมูล (Collection of Data)

                             2. การนำเสนอข้อมูล (Presentation of Data)

                             3. การวิเคราะห์ข้อมูล (Analysis of Data)

                             4. การตีความหมายของข้อมูล (Interpretation of Data)

ข้อมูล(Data) หมายถึง รายละเอียดข้อเท็จจริงของสิ่งต่าง ๆ ทั้งที่เป็นรูปธรรม และนามธรรมซึ่งตรงกับสิ่งที่ผู้วิจัยต้องการศึกษา

   ประเภทของวิชาสถิติ แบ่งประเภทตามลักษณะของข้อมูลได้เป็นสองประเภทคือ

               1 สถิติเชิงอนุมาน (Inductive Statistics) หมายถึง สถิติที่ใช้จัดกระทำกับข้อมูลที่ได้มาเพียงบางส่วนของข้อมูลทั้งหมด

               2 สถิติเชิงบรรยาย (Descriptive Statistics) หมายถึง สถิติที่ใช้จัดกระทำกับข้อมูลที่ได้มาเฉพาะเรื่องใดเรื่องหนึ่ง

การนำเสนอข้อมูล หมายถึง การจัดระบบข้อมูลให้เป็นหมวดหมู่ เป็นประเภท ตามลักษณะของการวิจัย เพื่อความชัดเจนในการวิเคราะห์ข้อมูลและการแปล ความหมายของข้อมูล

               การแจกแจงความถี่ (Frequency distribution table) จำแนกออกเป็นดังนี้คือ

              1. ข้อมูลดิบ (raw data) เป็นข้อทูลที่มาจากการเก็บรวบรวมจากแหล่งต่าง ๆ โดยยังไม่ไก้จัดเป็นหมวดหมู่

              2. อันตรภาคชั้น (class interval) คือช่วงหรือกลุ่มของคะนนที่แบ่งออกเป็นชั้น ๆ ของตารางแจกแจงความถี่

              3. ความถี่ (frequency) คือตัวเลขที่แสดงจำนวนข้อมูลที่มีอยู่ในแต่ละอันตรภาคชั้น

              4. การแจกแจงความถี่ (frequency distribution) คือการนำข้อมูลที่เก็บรวบรวมไว้มาจัดให้เป็นระเบียบเรียงลำดับค่าให้เป็นหมวดหมู่เพื่อความสะดวกในการวิเคราะห์ข้อมูล

              5. ตัวแปร (variable) ในทางสถิติแบ่งออกเป็น 2 ประเภทคือ

                             5.1 ตัวแปรเชิงปริมาณ เช่น อายุ น้ำหนัก ส่วนสูง รายได้ ฯลฯ

                             5.2 ตัวแปรเชิงคุณภาพ เช่น วุฒิ ศาสนา เพศ เชื้อชาติ ฯลฯ

     ความหมายของที่ใช้ในตารางแจกแจงความถี่

คะแนน	จำนวนนักเรียน
20-29	8
30-39	12
40-49	17
50-59	10
60-69	8
รวม	55

 -  เช่น ขอบลางของอันตรภาคชั้น 40-49 คือ  

-  เช่น ขอบบนของอันตรภาคชั้น 50-59   คือ   

                                             -  ความกว้างของอันตรภาคชั้น (I) = ขอบบน - ขอบล่าง 

                                                            เช่น ความกว้างของอันตรภาคชั้น  60-69 คือ  69.5-59.5= 10

                                            - ในกรณีที่ความกว้างของอันตรภาคชั้นเท่ากันทุกชั้น

                                            - ความกว้างของอันตรภาคชั้น = ผลต่างของค่าน้อยที่สุดของชั้นที่อยู่ติดกัน

                                                        หรือ   = ผลต่างของค่ามากที่สุดของชั้นที่อยู่ติดกัน

                                                        หรือ   = ผลต่างของจุดกึ่งกลางของชั้นที่อยู่ติดกัน

                                                           หรือ      เช่น  จุดกึ่งกลางของอันตรภาคชั้น  50-59 คือ  

หลักการสร้างตารางแจกแจงความถี่

              1. พิจารณาจำนวนข้อมูลดิบทั้งหมดว่ามีมากหรือน้อยเพียงใด

              2. หาค่าสูงสุดหรือต่ำสุดของข้อมูลดิบที่มีอยู่

              3. หาค่าพิสัยของข้อมูลนั้นจากสูตร

               4. พิจารณาว่าจะแบ่งเป็นกี่ชั้น (นิยม 5 - 15 ชั้น)

               5. หาความกว้างของแต่ละอันตรภาคชั้น จากสูตรนิยมปรับค่าให้เป็น 5 หรือ 10

              6. ควรเลือกค่าที่น้อยที่สุด หรือค่าที่มากที่สุดของอันตรภาคชั้นให้เป็นค่าที่สังเกตได้ง่าย ๆ

              ฮิสโตแกรม (Histogram) หรือ แท่งความถี่ คือ การแจกแจงความถี่ข้อมูลโดย ใช้กราฟแท่ง เพื่อให้เกิดความเป็นรูปธรรมของข้อมูลมากยิ่งขึ้นและง่ายต่อการวิเคราะห์ หรือตีความหมายข้อมูลค่ากลางของข้อมูล มีทั้งหมด 6 ชนิด

              1. ค่าเฉลี่ยเลขคณิตหรือตัวกลางเลขคณิต (arithmetic mean)

              2. มัธยฐาน (median)

              3. ฐานนิยม (mode)

              4. ตัวกลางเรขาคณิต (geometric mean)

              5. ตัวกลางฮาโมนิค (harmonic mean)

              6. ตัวกึ่งกลางพิสัย (mid-range

      ค่าเฉลี่ยเลขคณิตหรือตัวกลางเลขคณิต(arithmetic mean)หลักในการหาค่าเฉลี่ยเลขคณิต

          1. นำข้อมูลทั้งหมดมารวมกัน

          2. นำผลรวมที่ได้จากข้อ 1 มาหารด้วยจำนวนข้อมูลทั้งหมด

          3. ผลหารที่ได้ในข้อ 2 คือ ค่าเฉลี่ย

               มัธยฐาน(median) คือ ค่ากลางของข้อมูลที่อยู่กึ่งกลางของข้อมูลทั้งหมดหลังจากเรียงลำดับข้อมูลจากน้อยไปมากหรือจากมากไปน้อย แล้วการหาค่ามัธยฐาน  สามารถหาได้ดังนี้

              1. ถ้าจำนวนข้อมูลเป็นจำนวนคี่มัธยฐานคือค่าของข้อมูลตัวที่อยู่ตรงกลางพอดี

              2. ถ้าจำนวนข้อมูลเป็นจำนวนคู่มัธยฐานคือค่ากึ่งกลางของข้อมูล 2 จำนวนที่อยู่ตรงกลางของข้อมูลทั้งหมด

              3. ถ้าข้อมูลมี N จำนวนตำแหน่งมัธยฐานคือข้อมูลซึ่งอยู่ในตำแหน่ง   

ตัวอย่าง จงหาค่ามัธยฐานของข้อมูล 3 , 7 19, 25, 12, 18 , 10

                              วิธีทำ   เรียงข้อมูลจากน้อยไปมากได้ 3 , 7, 10, 12, 18, 19, 25

                             ข้อมูลมีทั้งหมด 7 ตัว เรียงข้อมูลแล้วตัวเลขที่อยู่ตรงกลางคือ

                             ตัวเลขตำแหน่งที่ 4 หรือจะใช้สูตรข้างบนได้

                             ตัวเลขตำแหน่งที่ 4 คือ 12 เป็นมัธยฐาน

ฐานนิยม(mode) คือ ข้อมูลที่มีความถี่มากสุด  หรือข้อมูลซ้ำกันมากที่สุด ในข้อมูลชุดหนึ่งๆ อาจจะมีฐานนิยมมากกว่า 1 ค่าก็ได้

                              ตัวอย่าง                จงหาฐานนิยมของข้อมูลชุดนี้ 3, 2, 5, 3, 3, 3, 3, 3, 3, 3, 5

                              วิธีทำ                    - เรียงข้อมูลใหม่จะได้ 2, 3, 3, 3, 3, 3, 3, 3, 3, 5, 5

                                                           - จากการเรียงข้อมูลใหม่แล้วจะเห็นว่า 3 เป็นข้อมูลที่มีความถี่มากสุด

                                                           ฐานนิยมของข้อมูลคือ 3

    

ตัวอย่าง  กำหนดข้อมูลชุดหนึ่งดังนี้คือ  7, 11, 19, 22, 7, 19, 17, 11,12, 11, 19

                             วิธีทำ     - เรียงข้อมูลใหม่จะได้ 7, 7, 11, 11, 11, 12, 17, 19, 19,19,22

                                            - จากการเรียงข้อมูลใหม่แล้วจะเห็นว่าข้อมูลที่มีความถี่มากสุดมี 2 จำนวนคือ 

11  และ  19

                            ฐานนิยมของข้อมูลคือ 11  และ  19

               หมายเหตุ  ในกรณีชุดข้อมูลชุดหนึ่งมีข้อมูลทุกตัวเท่ากันหมด  ในลักษณะเช่นนี้เราถือว่าข้อมูลชุดนี้ไม่มีฐานนิยม  เช่น:-3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5,  เป็นต้น

ค่าเฉลี่ยกรณีแจกแจงความถี่

                             สูตรค่าเฉลี่ยเลขคณิต  

                                   -  เมื่อ f คือ ความถี่ (จำนวน)

                                   -  N คือ จำนวนทั้งหมด

               ตัวอย่าง ตารางต่อไปนี้เป็นตารางแจกแจงความถี่ของอายุหลอดไฟฟ้าจำนวน 40 ดวง จงหาค่าเฉลี่ยเลขคณิตของอายุของหลอดไฟฟ้า

                 

วิธีทำ  เขียนตารางใหม่เพื่อหา fx  ได้ดังนี้

-  จากสูตรค่าเฉลี่ยเลขคณิต  

            -   แทนค่าในสูตร    

              อายุเฉลี่ยของหลอดไฟฟ้า = 131 

 

 

 

 

 

 

 

 

 

 

แนวข้อสอบคํานวณ สถิติ

1. ข้อมูลชุดหนึ่งมีดังนี้ 3, 7, 2, 5, 8 และ 10 จงหามัชฌิมเลขคณิตของข้อมูลชุดนี้

วิธีทํา

   ค่ามัชฌิมเลขคณิต = ผลรวมของข้อมูลทั้งหมด หารด้วยจํานวนของข้อมูล

   X = Σ x /n ถ้าข้อมูลแจกแจงความถี่ใช้ X = Σ fx /n

   = (3+7+2+5+8+10) = 5.8

                      6

2. จากข้อมูลต่อไปนี้ จงหาพิสัยของข้อมูล 100, 121, 99, 87, 86, 82, 111, 118, 120, 83, 170, 109, 130

วิธีทํา

   พิสัย = ค่าสูงสุด – ค่าต่ำสุด

        170 – 82 = 88

3. มัธยฐาน คือข้อมูลที่มาเรียงลําดับแล้วอยู่ตรงกลาง

   เช่น มัธยฐานของข้อมูล 2, 3, 5 ,6,8 คือ 5

    มัธยฐานของข้อมูล 1, 4, 5,7,8,9 คือ 5+7 = 6

                                                                2

4. ฐานนิยมคือ ข้อมูลที่มีความถี่มากที่สุด

   เช่น ฐานนิยมของข้อมูล 3, 8, 5, 6, 4, 5 คือ 5

5. ทอดลูกเต๋าเที่ยงตรง 1 ลูก ให้ E₁ เป็นเหตุการณ์ที่ได้แต้มตั้งแต่ 2 ขึ้นไป และให้ E₂ เป็นเหตุการณ์ที่ได้แต้มที่หารด้วย 2 ลง

ตัวจงหาตุการณ์ E₁ U E₂

วิธีทํา

   E₁ เป็นเหตุการณ์ที่ได้แต้มตั้งแต่ 2 ขึ้นไป จะได้ E₁ = {2, 3, 4, 5, 6}

   E₂ เป็นเหตุการณ์ที่ได้แต้มที่หารด้วย 2 ลงตัว จะได้ E₂ = {2, 4, 6 }

                                                                                 E₁ U E₂ = {2, 3, 4, 5, 6}

6. ทอดลูกเต๋าเที่ยงตรง 1 ลูกให้ E₁ เป็นเหตุการณ์ที่ได้แต้มตั้งแต่ 2 ขึ้นไป และให้ E₂ เป็นเหตุการณ์ที่ได้แต้มที่หารด้วย 2 ลงตัว

จงหาเหตุการณ์ E₁E₂

วิธีทํา

          E₁ เป็นเหตุการณ์ที่ได้แต้มตั้งแต่ 2 ขึ้นไป จะได้ E₁ = {2, 3, 4, 5, 6}

         E₂ เป็นเหตุการณ์ที่ได้แต้มที่หารด้วย 2 ลงตัว จะได้ E₂ = {2, 4, 6 }

                                                                                     E₁ E₂ = {2, 4, 6}

 

7. ข้อมูลจากตาราง จงหาความน่าจะเป็นที่สุ่มตัวอย่างมา 1 คน พบว่าเป็นมะเร็งและสูบบุหรี่

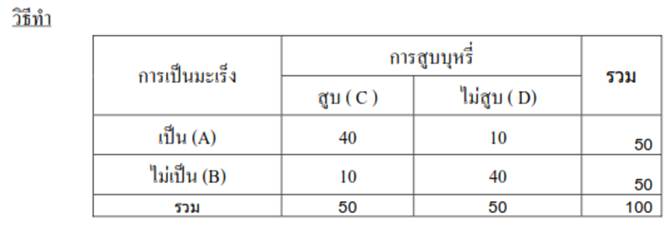
ความน่าจะเป็น P (C A) = 40/100 = 0.4

8 . ข้อมูลจากตาราง จงหาความน่าจะเป็นที่สุ่มตัวอย่างมา 1 คน พบว่าเป็นมะเร็งหรือสูบบุหรี่

ความน่าจะเป็น P {AU (BC)} = (50+10) /100 = 0.6

9. ทอดลูกเต๋าเที่ยงตรง 2 ลูก ความน่าจะเป็นที่ได้แต้มมีค่ารวมกัน 9 มีค่าเท่ากับเท่าใด

วิธีทํา

   จํานวนครั้งของการทอดลูกเต๋า S = 6 x 6 = 36

   แต้มลูกเต๋ารวมกันเท่ากับ 9 E = { 3-6, 4-5, 5-4, 6-3} = 4 ครั้ง

   ความน่าจะเป็น P(E) = 4/36 หรือ 1/9

10. ทอดลูกเต๋าเที่ยงตรง 2 ลูก ความน่าจะเป็นที่ได้แต้มมีค่ารวมกัน 7 มีค่าเท่ากับเท่าใด

วิธีทํา

   จํานวนครั้งของการทอดลูกเต๋า S = 6 x 6 = 36

   แต้มลูกเต๋ารวมกันเท่ากับ 7 E = { 1-6, 2-5, 3-4, 4-3, 5-2, 6-1 } = 6 ครั้ง

   ความน่าจะเป็น P(E) = 6/36 หรือ 1/6

11. ทอดลูกเต๋าเที่ยงตรง 2 ลูก ความน่าจะเป็นที่ได้แต้มมีค่ารวมกัน 7 มีค่าเท่ากับเท่าใด

ตอบ 1/16

วิธีทํา สูตรคือเหตุการณ์ที่เราสนใจหารด้วยเหตุการณ์ที่จะเกิดขึ้นหรือเป็นไปได้ทั้งหมด

สิ่งที่เราสนใจหรือต้องการคือการจับคู่ของลูกเต๋า2ลูกที่มีแต้มรวมกันได้ 7 ได้แก่ (1,6) (2,5) (3,4) (4,3) (5,2) (6,1) มีทั้งหมด 6 คู่

เหตุการณ์ที่เป็นไปได้ ลูกเต๋ามี 6 หน้า 6x6 = 36 ครั้ง แทนที่ในสูตร 6/36 ตัดกันให้เหลือตัวเลขน้อย เท่ากับ 1/6

12 . การแข่งขันกีฬาสีระหว่างทีม ก. กับทีม ข. พบว่าโอกาสที่ทีม ก. จะชนะในการแข่งขันแต่ละครั้งนั้นเท่ากับร้อยละ 60 ถามว่าในการแข่งขันกัน 5 ครั้ง ความน่าจะเป็นที่ทีม ก. จะชนะ 2 ครั้งเป็นเท่าใด

วิธีทํา

1.คํานวณจากสูตร P(X=x) = ⁿC_xp^x(1-p)^n-x ; x=0,1,2,..,n

  จํานวนการแข่ง                                               n =5

  โอกาสที่ทีม ก. ชนะ                              p = 0.6

  ความน่าจะเป็นที่จะชนะ             x = 2

      

 

 

 

 

 

2.คํานวณจากการเปิดตาราง จะต้องทราบค่า b(x, n, p)

  โดยค่าที่ได้จากโจทย์ n=5 p=0.6 x=2 หรือ b(2, 5, 0.6)

  แต่ตารางมีค่า p ถึงแค่ 0.5 เพราะฉะนั้นจะต้องแปลงค่า เป็น b(n-x, n, 1-p)

  ค่าที่ใช้เปิดตารางได้คือ b(5-2, 5, 1-0.6) = b(3, 5, 0.4) = 0.2304

  5c2 = 5!/(2!(5-2)!)

      = 5!/(2!3!)

      = (5x4x3!) / 2!3!

      = 5x4/2x1= 10

 

13. จากสถิติการคลอดที่โรงพยาบาลแห่งหนึ่งพบว่า ใน1 ปีมีผู้มาคลอด 1,200 ราย โดยเฉลี่ยพบว่าเป็นเด็กตายคลอดร้อยละ 1 จงหาค่าเฉลี่ยของจํานวนเด็กตายคลอดต่อเดือน

        = 1200/12 = 100

                    100x (1/100) = 1 คนต่อเดือน

 

14. ทอดลูกเต๋าเที่ยงตรง 2 ลูก ความน่าจะเป็นที่ได้แต้มมีค่ารวมกัน 7 มีค่าเท่ากับเท่าใด

     วิธีทํา สูตรคือเหตุการณ์ที่เราสนใจหารด้วยเหตุการณ์ที่จะเกิดขึ้นหรือเป็นไปได้ทั้งหมด

     สิ่งที่เราสนใจหรือต้องการคือการจับคู่ของลูกเต๋า2ลูกที่มีแต้มรวมกันได้ 7 ได้แก่ (1,6) (2,5) (3,4) (4,3)     

     (5,2) (6,1) มี

      ทั้งหมด 6 คู่ เหตุการณ์ที่เป็นไปได้ลูกเต๋ามี 6 หน้า 6x6 = 36 ครั้ง แทนที่ในสูตร 6/36 ตัดกันให้เหลือ   

     ตัวเลขน้อย เท่ากับ 1/6

15. จากสถิติการคลอดที่โรงพยาบาลแห่งหนึ่งพบว่าใน 1 ปี มีผู้มาคลอด 12,000 ราย โดยเฉลี่ยพบว่าเป็นเด็กตายคลอดร้อยละ 0.1 จงหาความแปรปรวนของจํานวนเด็กตายคลอดต่อเดือน

          เป็นการแจกแจงปังซง ค่าเฉลี่ย = ความแปรปรวน = np

       ผู้มาคลอดต่อเดือน = 12000/12 =1000 คน

                       = 1000x (0.1/100) = 1

16. สัมประสิทธิ์แห่งการกระจาย = S x 100

                                                        x

    ค่านี้อาจเรียกได้อีกชื่อหนึ่งว่า “สัมประสิทธิ์ของความแปรปรวน”(coefficient of variation, C.V.)

จะได้ CVก = (5/20) x 100 = 25

จะได้ CVข = (3/24) x 100 = 12.5

ดังนั้น ห้อง ก มีการกระจายมากกว่า ห้อง ข